BASIC KNOWLEDGE ON LCM

The term “Least Common Multiple” is represented as LCM. The smallest integer that may be divided by both integers is called the least common multiple of two integers. It can be done with two or even more numbers or fractions. To calculate the lcm of two digits, there are several techniques. The combination of the maximum power of the identical prime factors is the LCM of such integers, which is one of the best and easiest ways to find it.

What do you understand about LCM?

In the world of mathematics, the least common multiple is shortened as LCM. The lowest number amongst common multiples of two or more numbers is called the least common multiple. Think about two integers, for example, 3 and 7. Every pair of multiple sets will be unique.

We know that the multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, and so on.

Whereas, the multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, and so on.

In the given multiples if you see correctly then you will be able to spot the common multiples of 3 and 7, which is 21. Whereas, the highest common multiple of 3 and 7 till 70 is 63. This is because, 3 × 21 = 63 and 7 × 9 = 63.

So, we can say that the least common multiple of 3 and 7 is 21. While writing the terms of LCM, it can be mentioned as LCM (3, 7) = 21.

What is the best way to locate LCM?

There are several ways of calculating the LCM of integers. Finding the least common multiple of two integers can be done in one of three ways. Following are certain instances of each technique.

1. LCM by Division Method
2. LCM by Listing Method
3. LCM by Prime Factorization

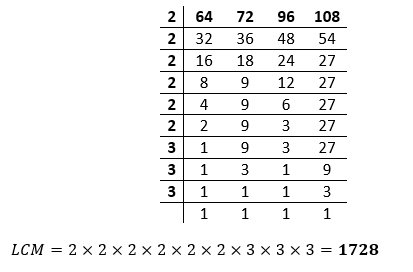
1. LCM by Division Method

We split the values by a single prime number, and the LCM of all those numbers is calculated using these prime factors. Follow the instructions below to determine the LCM of two digits utilizing the division method:

• Method 1: Determine a prime number that is a factor of at minimum one of the numbers provided. Place this prime number to the left of the numbers provided.

• Method 2: Divide the number by the prime number in step 1 and put the quotient beneath. If the prime number from step 1 would not be a factor of the integer, leave the number in the row beneath alone. Repeat the same steps until just one is left in the last line.

2. LCM by Listing Method

We may identify the common multiples of two or more integers by utilizing the list out the frequent multiples technique. The least common multiple is chosen among these common multiples, as well as the LCM of two integers can therefore be determined. Follow the instructions underneath to find the LCM of the two integers A and B using the listing technique:

• Method 1: Write down the first few A and B multiples.

• Method 2: Make a list of the frequent multiples of both integers.

• Method 3: Select the least common multiple in step three. The LCM of the two integers is the lowest common multiple.

3. LCM by Prime Factorisation

We can determine the prime factors of integers utilizing the prime factorization technique, and we can use all those prime factors to determine the LCM of all those integers. Follow the instructions underneath to determine the LCM of two integers utilizing the prime factorization technique:

• Method 1: Write the numbers as prime factors.

• Method 2: The sum of all prime factors is the LCM of the two numbers provided. (Common factors, nevertheless, would only be mentioned once.)

CONCLUSION

It is very much important to determine the LCM factors accurately. There is another terminology which is named HCF, which stands for the highest common factor. So you need to understand the basic difference between LCM and HCF as well.